
Melanie King
Assistant Professor of Mathematics, Cornell College
Offering resources to the community so that basic math becomes advanced analytical skill.
ABOUT ME
I am a PhD graduate in Applied Mathematics from the University of Iowa, Cornell College Assistant Professor, and Solon, IA resident. I've lived in Iowa for 11 years, but I am originally from Atlanta, GA. I also completed a one year post-bac program at Smith College in Northampton, Massachusetts.I've been teaching at Cornell College for FIVE YEARS. At Cornell, we teach on a block plan calendar, where one course is complete in 18 days. I've taught a very wide range of content from algebra and pre-calculus, calculus multiple and single variable to more general applied mathematics course.I really enjoy creating ACTIVITIES for my courses, they are a cornerstone of my instruction. I believe that these assignments are opportunities for students to engage in inquiry and problem-solving, learning using their own understanding and not just replicating my steps.Although I am immersed in the world of mathematics, my first love is LEARNING. I think about the process of knowledge construction; How does anyone know anything? A bit of a metacognitive question, I know, but one I turn over in my mind all the time.
GENERAL INQUIRIESIf you have shared interests or would like to follow up about anything, contact me via this form!

Skill Development Tutoring
Dates: Late July/Aug. Exact dates TBD.
Location: TBD
Time Slot 1: 9:00am-10:00am
Time Slot 2: 10:00am-11:00am
Cost: $35 per hour.
Three maximum participants in a 1 hour time slot.
Algebra Intensive
Dates: Mon. July 21st - Fri. July 25th
Location: TBD
Time: 9:30am-11:00am
COST: TBD
Twelve maximum participants
Click the link below if you would like to be notified when more information about these programs and/or registration becomes available.
From the Mind of Dr. King
Summer 2014 before starting graduate school.
Blog Topics
| How do mathematicians think? |
|---|
| I had NO IDEA when I decided to major in mathematics at Mercer University. Moreover, I certainly didn't know what I was getting into when I entered graduate school in Fall 2014. It took just one semester for me to observe that mathematicians were exactly what I had seen on tv: brainy, logical, mystical, accurate geniuses. Did anyone else watched the show Numbers on CBS? |
| During my first year of graduate school, I STRUGGLED with learning mathematical reasoning and logic, as it was presented in the most abstract way. After "failing" a few exams, I had to start asking the question "How do they know what to do? How did they solve the problem?", not just "What is the answer?". What I had to learn was how to solve problems on my own without any work or steps shown to me first. |
| Now, years later, I can answer this question with some level of authority. Indeed, I've spoken about it to a group of home-schooled middle school students in Marion, IA. I've written an article about it in the Cornell Newsletter. I've also found other people who have grappled with similar questions. I enjoyed using the book Math with Bad Drawings by Ben Orlin in my Math for Liberal Arts course in the Spring of 2025. |
Fall 2019
How Learning WorksI was a Center for Career Teaching Graduate Fellow at the University of Iowa in the academic year 2019-2020. In the book, "How Learning Works" by Susan Ambrose et. al., I discovered a graphic representing expert knowledge and novice knowledge.
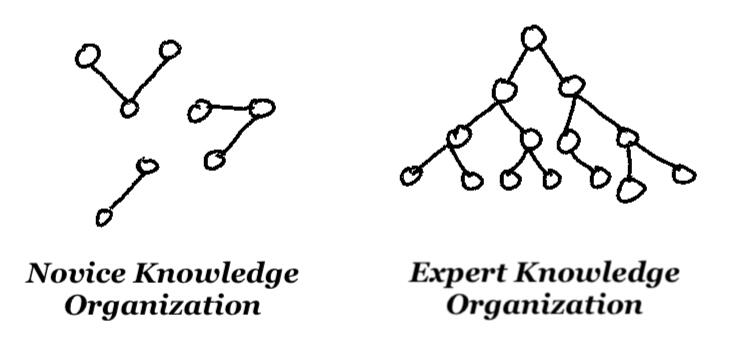
At the time, this graphic was validation that I was right to ask the question “How do mathematicians think?” I was unknowingly asking how their information was organized to be a useful system for solving problems. Admittedly, it took a lot of effort and time for me to become a decent problem solver in the mathematical sense. I kept running into “dead ends” in my knowledge bank, where my mind would go blank. I didn’t have the next step. This is another layer of learning how to problem solve: How do you get unstuck?Now, the graphic informs how I visualize what goes on in my head versus what goes on in the student’s heads when they are learning in my math classes. A lot of the time, when I am teaching in class, I am giving students the “dots” for their network, i.e. the bits of information for the topic at hand. Moreover, doing some problems and having students practice these exact problems is like making the three dot connections in the novice network, as the graphic shows above.One of my more lofty course objectives is to give students an opportunity to make deeper and more advanced connections with the content. I attempt to do this using open-ended activities, where students must come up with the knowledge/information they need to know and how to use it to reach a conclusion. One of my challenges with these activities is to give them a problem that is within their capabilities, but interesting enough to be engaging.
Upcoming Posts!- How to teach mathematics, a literature review
May 2025
How important is algebra really?
What is algebra? It’s just rules about numbers and combining them using the operations addition, subtraction, multiplication, and division. Really, that’s all. You may say, “BUT there are so many more symbols in algebra than just the four operations!” To which I reply, yes, but they stem from the four operations. For example, exponents are symbols that indicate repeated multiplication. Then, you get roots because you need a way to undo repeated multiplication. Then, you introduce unknown numbers (variables) and you can combine them with operations to make expressions, but these are still just numbers. All this gooba-de-gook here is just a NUMBER.
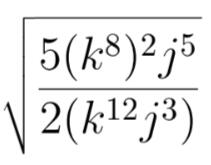
When you compare numbers, you get equations. When you have two unknown numbers (x and y), but one of the numbers (y) depends on the other (x) is changed, you get functions. But what if one number (z) depends on how TWO numbers are changed (x and y), then you get a multivariable function. And alas, we have taken the journey from 8th grade math to freshman, sophomore level college math in a matter of 10 sentences. (As an aside, I will note that algebra also includes polynomials, rational, exponential, logarithmic, and trigonometric functions. Do all these stem from the numbers and operations addition, subtraction, multiplication and division?? Yes, yes they do.)So, how important is algebra really? Until 2 years ago, I thought it was the most important skill to have for anyone working with mathematics in any way. There is a correlation, in my head, between algebra skills and problem-solving skills, since algebra is the first advanced playground for mathematical problem-solving most students encounter. But algebra is in a gun-slinging duel with technology (calculators and Desmos), which can do algebra computations in a matter of seconds. Students know this and, I have found in my short stint of teaching, this is enough for them not to buy into the need to really learn algebra. It has been pretty discouraging to see as a professor, because without student buy-in, learning can’t occur. And I started to question if students can get by primarily using technology for answers.I am dedicating Summer 2025 to diving into this question. I will collect newspaper articles, journal and research articles, national reports, and names/contacts of people engaging in this conversation. In fact, WE could start this journey together, with say this article written in The Hechinger Report, a “national nonprofit newsroom that reports on one topic: education.” The internet will be my accountability partner this summer. I’ll keep you posted.

After Frans Hals, Public domain, via Wikimedia Commons
Upcoming Posts!- My favorite mathematician
- Hyperbolic Geometry